Making My Own Autograd System
How Autograd Systems Work
Many people who "understand" "AI" do nothing but call libraries someone
else has written for them. In fact, I would say the vast majority of "AI Experts"
do nothing but re-arrange existing solutions with potentially novel data.
Without any real understanding of the mechanisms they're using they cannot develop anything
new or interesting. Their skills are so dependent on arbitrary decisions and libraries,
that the vast majority of them wouldn't be able to do even the simplest machine learning tasks
if you took them out of their Python interpreter. People who operate like that will never be mages
and will never understand the arcane arts.
In an effort to avoid being like these sad, sorry, pathetic, non-mages, I have spent a large
amount of my life working with what, at the time, I considered to be the bare minimum, an autograd
library. This ensured that I at the very least understood the forwards pass, optimizers, normalization,
and regularization techniques I was using. This served me well, and when I left the comfort of my own
notebook I was always able to export the weights and write the forwards pass in whatever environment just
fine.
Of course, there was a critical mistake in the making- I was using a library (disgusting behaviour).
To remedy this and atone for my sins against The Computer, I have decided to write my own
autograd library. To prove that at the very least I understand the basics of how one works.
Compute Graphs and The Forwards Pass
This should be a familiar topic, given some math expression like:
3*x + x^2 - sqrt(x)
We can break it up into an easier to parse syntax, such as:
plus(plus(times(3, x), pow(x, 2)), neg(sqrt(x)))
Which can be turned into a binary tree where each node represents an operation,
the left and right hand branches represent the expression they operate on.
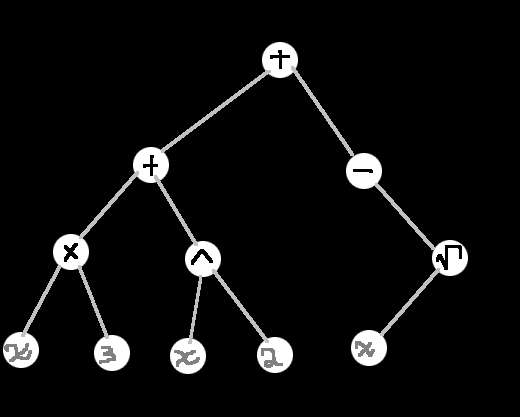
I made this in Tux Paint.
So we can pack that data into a graph using a structure something like this
struct Node {
float value = 0.0f;
float grad = 0.0f;
Operation oper = NONE;
std::shared_ptr lhs = nullptr;
std::shared_ptr rhs = nullptr; // leave null for single operations
};
enum Operation {
MULT,
ADD,
POW,
EXP,
LOG,
SIN,
COS,
TANH,
DIV,
RELU,
NONE
};
Then computing the expression is pretty simple, we just go through all the nodes
and do their operations. I'll write this as simply as possible, by using a set
to prevent calculations on re-visited nodes. But it's possible (and faster) to
go through them all without repeating.
void updateValue(NodePtr n, std::unordered_set& visited) {
if (!n || visited.count(n)) return;
visited.insert(n);
if (n->oper == NONE) return;
if (n->lhs) updateValue(n->lhs, visited);
if (n->rhs) updateValue(n->rhs, visited);
switch (n->oper) {
case MULT:
n->value = n->lhs->value * n->rhs->value;
break;
case ADD:
n->value = n->lhs->value + n->rhs->value;
break;
case POW:
n->value = pow(n->lhs->value, n->rhs->value);
break;
case EXP:
n->value = exp(n->lhs->value);
break;
case LOG:
n->value = log(n->lhs->value);
break;
case SIN:
n->value = sin(n->lhs->value);
break;
case COS:
n->value = cos(n->lhs->value);
break;
case TANH:
n->value = tanh(n->lhs->value);
break;
case DIV:
n->value = n->lhs->value / n->rhs->value;
break;
case RELU:
n->value = std::max(0.0f, n->lhs->value);
break;
default:
break;
}
}
float forward(float root) {
std::unordered_set visited;
updateValue(root, visited);
return root->value;
}
If we want to optimize a function we use a lot, we can put it in here as a single operation
instead of making that operation out of many smaller nodes.
The parts we have made so far are called the forwards pass, because we're calculating things in the
normal order. Up to now I hope you can agree things are pretty simple, maybe even obvious.
Surprisingly though, they don't actually get much harder than that.
Backpropagation and The Power Rule
You probably learned from an illegally downloaded caluclus textbook about derivatives. When people
in machine learning say "gradient" they mean derivatives. Every time they have more than one derivative
they like to call it a gradient. This is because it makes them sound smarter. Anyway, the term "derivatives"
works just fine.
Recalling the lesson you got from that illegal textbook, when you take the derivative of something
you have to do the derivative bit for the operation, and his neighbor, then multiply.
That was called the chain rule.
Apart from the chain rule, we have a bunch of rules for each operation. These can be sussed out
using the definition of the derivative, but lets not bother.
// Backward pass with visited set
void updateBack(NodePtr n, std::unordered_set& visited) {
if (!n || visited.count(n)) return;
visited.insert(n);
if (n->oper == NONE) return;
switch (n->oper) {
case MULT:
n->lhs->grad += n->rhs->value * n->grad;
n->rhs->grad += n->lhs->value * n->grad;
updateBack(n->lhs, visited);
updateBack(n->rhs, visited);
break;
case ADD:
n->lhs->grad += n->grad;
n->rhs->grad += n->grad;
updateBack(n->lhs, visited);
updateBack(n->rhs, visited);
break;
case POW:
if (n->lhs->value > 0) {
n->lhs->grad += n->rhs->value * pow(n->lhs->value, n->rhs->value - 1) * n->grad;
n->rhs->grad += log(n->lhs->value) * pow(n->lhs->value, n->rhs->value) * n->grad;
}
updateBack(n->lhs, visited);
updateBack(n->rhs, visited);
break;
case EXP:
n->lhs->grad += n->value * n->grad;
updateBack(n->lhs, visited);
break;
case LOG:
n->lhs->grad += (1 / n->lhs->value) * n->grad;
updateBack(n->lhs, visited);
break;
case SIN:
n->lhs->grad += cos(n->lhs->value) * n->grad;
updateBack(n->lhs, visited);
break;
case COS:
n->lhs->grad += -sin(n->lhs->value) * n->grad;
updateBack(n->lhs, visited);
break;
case TANH: {
NumKin t = tanh(n->lhs->value);
n->lhs->grad += (1 - t * t) * n->grad;
updateBack(n->lhs, visited);
break;
}
case DIV: {
NumKin a = n->lhs->value;
NumKin b = n->rhs->value;
n->lhs->grad += (1 / b) * n->grad;
n->rhs->grad += (-a / (b * b)) * n->grad;
updateBack(n->lhs, visited);
updateBack(n->rhs, visited);
break;
}
case RELU: {
n->lhs->grad += (n->lhs->value > 0 ? 1.0f : 0.0f) * n->grad;
updateBack(n->lhs, visited);
break;
}
default:
break;
}
}
void backpropagation(NodePtr root) {
root->grad = 1.0f;
std::unordered_set visited;
updateBack(root, visited);
}
void resetGraph(NodePtr root) {
// Make the graph ready to use again!
root->grad = 0;
// Reset all the values that aren't 'constants'
// we don't really need to do this
if (root->oper != NONE)
root->value = 0;
// Not just the root node, but the root women and root children
// too!
if (root->lhs) resetGraph(root->lhs);
if (root->rhs) resetGraph(root->rhs);
}
If you want to add an operation to this list it's pretty easy. Just go find the derivative rule
for that operation (you can steal them from
Wikipe-tan ),
then put it in here, and multiply it by n->grad. If you want to optimize a more
complex expression, then put the derivative of the whole expression in there.
Multi-Dimensional Operations
The elites don't want you to know this, but all those complicated linear algebra
operations are actually just short-hands for normal operations you could have understood
when you were a child. Mathematicians like to use complicated symbols because it hides
the fact that they aren't very smart.
So to implement them into our autograd engine, we'll just do them normally, instead of
being a complicated mathematician who is insecure and hides behind his fancy symbols.
using Vector = std::vector;
using Matrix = std::vector;
using Tensor3 = std::vector;
using Tensor4 = std::vector;
Matrix multMatrix(const Matrix& A, const Matrix& B) {
size_t m = A.size(); // Rows in A
size_t k = A[0].size(); // Cols in A == Rows in B
size_t n = B[0].size(); // Cols in B
Matrix C(m, std::vector(n));
for (size_t i = 0; i < m; ++i) {
for (size_t j = 0; j < n; ++j) {
NodePtr sum = multNodes(A[i][0], B[0][j]);
for (size_t l = 1; l < k; ++l) {
sum = addNodes(sum, multNodes(A[i][l], B[l][j]));
}
C[i][j] = sum;
}
}
return C;
}
Matrix im2col(const Tensor3& input, int kernel_h, int kernel_w, int stride = 1) {
int C = input.size();
int H = input[0].size();
int W = input[0][0].size();
int out_h = (H - kernel_h) / stride + 1;
int out_w = (W - kernel_w) / stride + 1;
int patch_size = C * kernel_h * kernel_w;
int num_patches = out_h * out_w;
Matrix cols(patch_size, Vector(num_patches));
int patch_idx = 0;
for (int i = 0; i < out_h; ++i) {
for (int j = 0; j < out_w; ++j) {
int col_pos = 0;
for (int c = 0; c < C; ++c) {
for (int kh = 0; kh < kernel_h; ++kh) {
for (int kw = 0; kw < kernel_w; ++kw) {
int h_idx = i * stride + kh;
int w_idx = j * stride + kw;
cols[col_pos][patch_idx] = input[c][h_idx][w_idx];
++col_pos;
}
}
}
++patch_idx;
}
}
return cols;
}
An Example
Let's put together an example using both our autograd system and Pytorch. Then
we can compare their outputs to see if we're on the right track.
void testFunction() {
// Create a 5x4 matrix A with values: sin(0.1 * i * j + 1)
std::vector> A(5, std::vector(4));
for (int i = 0; i < 5; ++i)
for (int j = 0; j < 4; ++j)
A[i][j] = constantNode(std::sin(0.1f * i * j + 1.0f));
// Create a 4x8 matrix B with values: cos(0.2 * i - 0.3 * j + 2)
std::vector> B(4, std::vector(8));
for (int i = 0; i < 4; ++i)
for (int j = 0; j < 8; ++j)
B[i][j] = constantNode(std::cos(0.2f * i - 0.3f * j + 2.0f));
// Matrix multiplication: (5x4) * (4x8) = (5x8)
auto C = multMatrix(A, B);
// Apply tanh to each output node and sum to create scalar loss
NodePtr loss = tanhNode(C[0][0]);
for (int i = 0; i < 5; ++i) {
for (int j = 0; j < 8; ++j) {
if (i != 0 || j != 0) {
loss = addNodes(loss, tanhNode(C[i][j]));
}
}
}
// Run forward and backward passes
forward(loss);
backpropagation(loss);
// Print gradients of A
std::cout << "Gradients of A:\n";
for (int i = 0; i < 5; ++i) {
for (int j = 0; j < 4; ++j) {
std::cout << A[i][j]->grad << "\t";
}
std::cout << "\n";
}
// Print gradients of B
std::cout << "\nGradients of B:\n";
for (int i = 0; i < 4; ++i) {
for (int j = 0; j < 8; ++j) {
std::cout << B[i][j]->grad << "\t";
}
std::cout << "\n";
}
}
import torch
import math
# Create A: 5x4 matrix with varied values
A = torch.tensor([
[math.sin(0.1 * i * j + 1) for j in range(4)]
for i in range(5)
], requires_grad=True)
# Create B: 4x8 matrix with varied values
B = torch.tensor([
[math.cos(0.2 * i - 0.3 * j + 2) for j in range(8)]
for i in range(4)
], requires_grad=True)
# Matrix multiplication
C = A @ B # Shape: (5x8)
# Use a non-linear scalar loss: sum(tanh(C))
loss = torch.tanh(C).sum()
# Backward pass
loss.backward()
# Print values and gradients of A
print("A values:")
print(A)
print("\nA gradients:")
print(A.grad)
# Print values and gradients of B
print("\nB values:")
print(B)
print("\nB gradients:")
print(B.grad)
Gradients of A:
0.61269 0.219674 -0.182099 -0.576613
0.582877 0.21873 -0.154137 -0.52086
0.565164 0.21403 -0.145636 -0.499497
0.557875 0.205803 -0.154473 -0.508591
0.559561 0.192885 -0.18148 -0.548611
Gradients of B:
0.147051 0.777565 3.37213 3.06425 0.656405 0.126285 0.0356017 0.01724
0.15991 0.848784 3.69551 3.35678 0.716248 0.137304 0.0386035 0.0186636
0.163341 0.868111 3.78739 3.44395 0.733957 0.140486 0.039448 0.0190548
0.157246 0.83497 3.6448 3.32286 0.70897 0.135735 0.038111 0.0184026
The Moral of The Story
The moral of the story is that I am smarter and cooler than everyone else.
Because I'm so smart and cool, you should take my advice, which is to
reconsider whether or not you need as many libraries as you think you do.
You should also consider the case where you didn't have those libraries, would
you still be able to cast your spells?
If you answered "no" to that last question, you are not a mage and you should
feel bad about yourself.
Continuation
I intend to continue this line of notes to the point that I can get a convolutional
network to run on the MNIST dataset with reasonable performance.
